Bất đẳng thức Cosi – Chứng minh, cho ví dụ và giải bài tập

Công thức bất đẳng thức Cosi, chứng minh bất đẳng thức cauchy-schwarz lớp 8, lớp 9. Ví dụ và giải bài tập bất đẳng thức Côsi. 

Bất đẳng thức Cosi là một trong những bất đẳng thức quan trọng và cơ bản trong toán học, đặc biệt trong đại số và giải tích. Tên gọi khác của bất đẳng thức Cosi là bất đẳng thức Cauchy-Schwarz hoặc bất đẳng thức Cauchy. Bất đẳng thức Cauchy được ứng dụng rộng rãi trong nhiều lĩnh vực như toán học thuần túy, vật lý, kinh tế học và các bài toán thực tế.

• Tìm hiểu thêm: Bất đăng thức là gì? Cho ví dụ về bất đẳng thức

Công thức bất đẳng thức Cosi

Công thức bất đẳng thức Cauchy tổng quát

Dạng cơ bản trong số học:

$$\frac{a_1 + a_2 + \cdots + a_n}{n} \geq \sqrt[n]{a_1 \cdot a_2 \cdot \cdots \cdot a_n}$$

​Trong đó: $a_1, a_2, \ldots, a_n$

là các số thực không âm. Dấu “=” xảy ra khi tất cả các số bằng nhau.

Dạng tổng quát trong không gian vector:

$$\mathrm{\mid }⟨u,v⟩{\mathrm{\mid }}^2\le \mathrm{\parallel }u{\mathrm{\parallel }}^2\mathrm{\parallel }v{\mathrm{\parallel }}^2$$

Trong đó: $u,v$ là các vector trong không gian Euclid, và dấu “=” xảy ra khi $u$ và $v$ cùng phương.

Dạng thường gặp trong các bài toán:

$${(\sum a_i{b}_i)}^2\le (\sum a_i^2)(\sum b_i^2)$$

Trong đó: $a_i, b_i$ là các số thực bất kỳ.

Công thức bất đẳng thức Cauchy cho 2 số dương

Bất đẳng thức Cauchy cho 2 số dương là trường hợp đặc biệt đơn giản nhất của bất đẳng thức Cauchy-Schwarz, được phát biểu như sau:

Cho $a$ và b là hai số dương, ta có:

$$\frac{a + b}{2} \geq \sqrt{ab}$$

Dấu bằng xảy ra khi và chỉ khi a=b.

Công thức bất đẳng thức cosi cho 3 số dương

Bất đẳng thức Cauchy cho 3 số dương là trường hợp mở rộng của bất đẳng thức trung bình cộng và trung bình nhân (AM-GM) áp dụng cho 3 số.

Cho a, b, c là ba số dương, ta có:

$$\frac{a + b + c}{3} \geq \sqrt[3]{abc}$$

Dấu bằng xảy ra khi và chỉ khi $a=b=c$.

Công thức bất đẳng thức Cauchy AM-GM

Bất đẳng thức Cosi AM-GM (Arithmetic Mean – Geometric Mean) là một trong những bất đẳng thức cơ bản và quan trọng trong toán học. Bất đẳng thức Cauchy AM-GM kết nối giữa trung bình cộng và trung bình nhân của các số dương.

Cho $a_1, a_2, \ldots, a_n$ là $n$ số thực dương. Khi đó:

$$\frac{a_1 + a_2 + \cdots + a_n}{n} \geq \sqrt[n]{a_1 a_2 \cdots a_n}$$

Dấu bằng xảy ra khi và chỉ khi $a_1 = a_2 = \cdots = a_n$

Bất đẳng thức AM-GM chỉ ra rằng trung bình cộng của n số thực dương luôn lớn hơn hoặc bằng trung bình nhân của chúng. Sự cân bằng (khi dấu “=”) đạt được khi tất cả các số bằng nhau.

Chứng minh bất đẳng thức Cosi (AM-GM)

Chứng minh bằng phương pháp số học

Xét trường hợp bất đẳng thức Cauchy cho hai số dương $a,b$:

=> Kết luận: Bất đẳng thức được chứng minh.

Chứng minh bằng phương pháp đại số

Bất đẳng thức Cosi tổng quát cho hai số dương $a,b$:

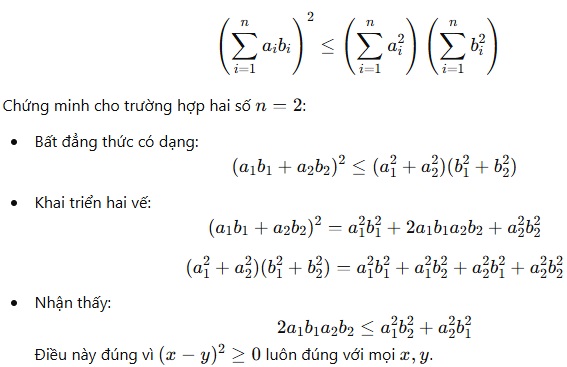
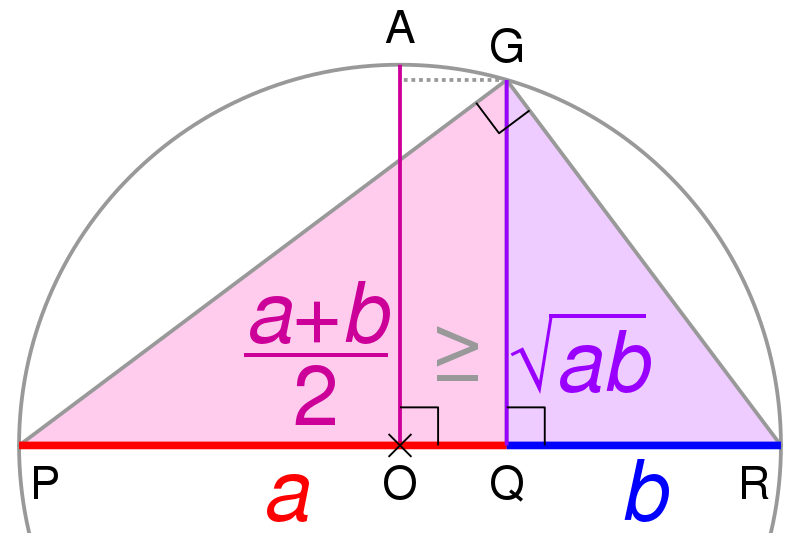
Chứng minh bằng phương pháp hình học

Bài tập về bất đẳng thức Cauchy (AM-GM)

Bài 1: Tìm giá trị nhỏ nhất của

$x + \frac{1}{x}$​ với x > 0.

Lời giải:
Áp dụng bất đẳng thức Cosi cho hai số dương x và $\frac{1}{x}$​:

$$\frac{x+\frac{1}{x}}{2}\ge \sqrt{x\cdot \frac{1}{x}}=1$$ $$\implies x + \frac{1}{x} \geq 2$$

Dấu bằng xảy ra khi $x = \frac{1}{x}$, tức là $x=1$.
Kết luận: Giá trị nhỏ nhất là 2, đạt được khi x=1.

Bài 2: Chứng minh rằng với mọi số dương $a,b,c$:

$$a+b+c\ge 3\sqrt[3]{abc}\mathrm{.}$$

Lời giải:
Áp dụng bất đẳng thức Cauchy cho ba số dương a, b, c:

$$\frac{a + b + c}{3} \geq \sqrt[3]{abc}$$

Nhân cả hai vế với 3, ta được:

$$a + b + c \geq 3\sqrt[3]{abc}.$$

Dấu bằng xảy ra khi $a=b=c$.

Kết luận: Bất đẳng thức được chứng minh.

Bài 3: Chứng minh rằng nếu $x,y>0$ thì:

$$x^3 + y^3 \geq xy(x + y).$$

Lời giải:
Áp dụng bất đẳng thức Cosi cho hai số $x^3$ và$y^3$:

$$x^3 + y^3 \geq 2\sqrt{x^3y^3} = 2(xy)^{\frac{3}{2}}.$$

Ta cần chứng minh:

$$2(xy)^{\frac{3}{2}} \geq xy(x + y).$$

Chia cả hai vế cho $xy$ (vì x, y>0), ta được:

$$2\sqrt{xy} \geq x + y.$$

Điều này đúng do bất đẳng thức Cosi:

$$\frac{x+y}{2}\ge \sqrt{xy}\mathrm{.}$$

Dấu “=” xảy ra khi $x=y$.

Kết luận: Bất đẳng thức được chứng minh.

Bài 4: Chứng minh rằng với mọi số dương a, b:

$$\frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b}.$$

Lời giải:
Áp dụng bất đẳng thức Cauchy cho $\frac{1}{a}$ và $\frac{1}{b}$:

$$\frac{\frac{1}{a} + \frac{1}{b}}{2} \geq \sqrt{\frac{1}{a} \cdot \frac{1}{b}}.$$

Nhân cả hai vế với 2:

$$\frac{1}{a} + \frac{1}{b} \geq 2\sqrt{\frac{1}{ab}}.$$

Vì $a + b \geq 2\sqrt{ab}$​, ta suy ra:

$$2\sqrt{\frac{1}{ab}} = \frac{4}{a + b}.$$

Do đó:

$$\frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b}.$$

Kết luận: Bất đẳng thức được chứng minh.

Bài 5: Cho $a,b,c>0$, chứng minh rằng:

$$\frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b} \geq \frac{3}{2}.$$

Lời giải:
Áp dụng bất đẳng thức Cauchy cho từng phân số:

$$\frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b} \geq \frac{(a + b + c)^2}{2(ab + bc + ca)}.$$

Ta có:

$$a + b + c \geq \sqrt{3(ab + bc + ca)}.$$

Thay vào, bất đẳng thức trở thành:

$$\frac{(a + b + c)^2}{2(ab + bc + ca)} \geq \frac{3}{2}.$$

Điều này đúng.

Kết luận: Bất đẳng thức được chứng minh.

Một số ví dụ về bất đẳng thức Cauchy-Schwarz

Ví dụ 1:
Chứng minh $\frac{3 + 12}{2} \geq \sqrt{3 \cdot 12}$.

Lời giải:

$$\frac{3 + 12}{2} = \frac{15}{2} = 7.5, \quad \sqrt{3 \cdot 12} = \sqrt{36} = 6$$

Vì 7.5 ≥ 6, bất đẳng thức được chứng minh.

Ví dụ 2:
Tìm giá trị lớn nhất của x khi $\frac{x + 9}{2} \geq 6$.

Lời giải:

$$\frac{x + 9}{2} \geq 6 \implies x + 9 \geq 12 \implies x \geq 3$$

Ví dụ 3: Cho a, b, c > 0 thỏa mãn $a+b+c=12$. Tìm giá trị lớn nhất của abc.

Lời giải: Áp dụng bất đẳng thức Cauchy, ta có:

$$\sqrt[3]{abc} \leq \frac{a + b + c}{3} = \frac{12}{3} = 4$$

$$\implies abc \leq 4^3 = 64$$

Dấu “=” xảy ra khi $a=b=c=4$.