Bất đăng thức là gì? Ví dụ và bài tập về bất đẳng thức

Tìm hiểu khái niệm bất đẳng thức là gì, các loại bất đẳng thức phổ biến, ứng dụng và ví dụ về bất đẳng thức trong toán học cũng như đời sống.

Hầu hết chúng ta đã quen thuộc với bất đẳng thức từ khi học phổ thông. Tuy nhiên, khái niệm này còn ẩn chứa nhiều điều thú vị và ứng dụng sâu rộng hơn. Trong bài viết này, chúng ta sẽ cùng khám phá định nghĩa bất đẳng thức là gì, các loại bất đẳng thức phổ biến và những ví dụ về bất đẳng thức nhé!

Bất đẳng thức là gì

1. Bất đẳng thức là gì?

1.1. Định nghĩa bất đẳng thức

Bất đẳng thức là một mối quan hệ giữa hai biểu thức toán học, trong đó chúng được so sánh với nhau bằng các ký hiệu:

• < (nhỏ hơn)
• > (lớn hơn)
• ≤ (nhỏ hơn hoặc bằng)
• ≥ (lớn hơn hoặc bằng)

Bất đẳng thức giúp xác định xem giá trị của một biểu thức có lớn hơn, nhỏ hơn hay bằng giá trị của biểu thức còn lại. Đây là một công cụ quan trọng trong toán học để giải quyết các vấn đề về so sánh và tìm kiếm giá trị tối ưu.

1.2. Ví dụ về bất đẳng thức

• a > b: Biểu thức này có nghĩa là giá trị của a lớn hơn giá trị của b.
• x + y ≤ z: Biểu thức này có nghĩa là tổng của x và y nhỏ hơn hoặc bằng giá trị của z.

Những biểu thức như vậy không chỉ xuất hiện trong lý thuyết toán học mà còn có nhiều ứng dụng thực tế trong phân tích dữ liệu, lập trình và nghiên cứu khoa học.

2. Phân loại bất đẳng thức

Bất đẳng thức được phân loại dựa trên cấu trúc, tính chất và mức độ phức tạp. Dưới đây là các loại bất đẳng thức phổ biến:

2.1. Bất đẳng thức cơ bản

Là các bất đẳng thức đơn giản, thể hiện mối quan hệ so sánh trực tiếp giữa hai số hoặc hai biểu thức.

Ví dụ: $3>2$, $5\le 7$.

2.2. Bất đẳng thức tuyến tính

Là bất đẳng thức trong đó các biến xuất hiện với bậc nhất (không có số mũ hoặc các phép toán phức tạp).

Ví dụ: $2x+3>5$.

2.3. Bất đẳng thức bậc hai

Liên quan đến các biểu thức chứa biến với bậc cao nhất là hai.

Ví dụ:

$x^2 + x – 2 ≥ 0$

2.4. Bất đẳng thức chứa dấu giá trị tuyệt đối

Xuất hiện trong các bài toán mà giá trị biểu thức được xác định theo khoảng cách đến điểm gốc.

$Ví\; dụ:$

$|x-3|<5$.$|x – 3| < 5$

2.5. Bất đẳng thức trong hình học

Mối quan hệ giữa các đoạn thẳng, góc, hoặc diện tích.

Ví dụ:

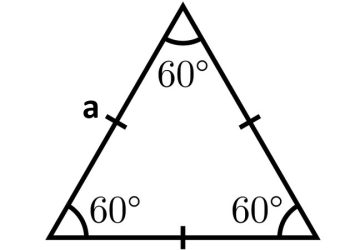
Trong một tam giác, tổng độ dài hai cạnh luôn lớn hơn cạnh còn lại (

2.6. Bất đẳng thức trong bất phương trình

Là những bất đẳng thức cần tìm nghiệm, thường xuất hiện trong các bài toán giải bất phương trình.

Ví dụ:

$x^2 – 4x + 3 < 0$

2.7. Bất đẳng thức Cauchy-Schwarz

Liên quan đến tích vô hướng trong đại số và hình học

Ví dụ:

$(a^2 + b^2)(x^2 + y^2) ≥ (ax + by)^2$

2.8. Bất đẳng thức AM-GM

Tổng trung bình cộng không nhỏ hơn trung bình nhân.

Ví dụ: 

$\frac{a + b}{2} ≥ \sqrt{ab}$

(với $a,b\ge 0$).

3. Tính chất của bất đẳng thức

Bất đẳng thức có nhiều tính chất quan trọng giúp chúng ta giải bài toán một cách dễ dàng và chính xác. Dưới đây là các tính chất cơ bản của bất đẳng thức:

3.1. Tính chất đối xứng

Nếu $a>b$, thì không thể có $b>a$.

Nếu $a=b$, thì cả hai bằng nhau, không có sự so sánh lớn hơn hoặc nhỏ hơn.

3.2. Tính chất cộng

Nếu $a>b$, thì $a+c>b+c$ (với $c$ là một số bất kỳ).

Tương tự, với $a<b$, cộng cùng một giá trị $c$ vào cả hai vế không làm thay đổi chiều của bất đẳng thức.

Ví dụ:

Nếu 3 > 2, thì $3+5>2+5$.

3.3. Tính chất nhân

Nhân với số dương

Nếu a > b và $c>0$, thì $a\cdot c>b\cdot c$.

Tương tự, nếu a < b, nhân cả hai vế với số dương vẫn giữ nguyên chiều bất đẳng thức.

Nhân với số âm

Nếu a > b và c < 0, thì $a\cdot c<b\cdot c$.

Khi nhân với số âm, chiều của bất đẳng thức sẽ đảo ngược.

Ví dụ:
Nếu $2>1$:

• Nhân với $3$: $2\cdot 3>1\cdot 3$.
• Nhân với $-2$: 2⋅(−2)<1⋅(−2).

3.4. Tính chất chia

Chia cho số dương

Nếu $a>b$ và $c>0$, thì

$\frac{a}{c} > \frac{b}{c}$

Chia cho số âm

Nếu $a>b$ và $c<0$, thì

$\frac{a}{c} < \frac{b}{c}$

​ (chiều bất đẳng thức đảo ngược).

Ví dụ:

Nếu 6 > 3:

Chia cho $2$:

$\frac{6}{2} > \frac{3}{2}$

Chia cho $-1$:

$\frac{6}{-1} < \frac{3}{-1}$

3.5. Tính chất bắc cầu

Nếu $a>b$ và $b>c$, thì $a>c$.

Nếu $a<b$ và $b<c$, thì $a<c$.

Ví dụ:

Nếu 5 > 3 và $3>1$, thì 5 > 1.

3.6. Tính chất bình phương

Nếu $a>b$ và $a,b\ge 0$, thì

2>b2a^2 > b^2

Nếu $a<b$ và $a,b\ge 0$, thì

$a^2 < b^2$

Lưu ý: Khi $a,b<0$, bình phương cả hai vế có thể làm mất chiều bất đẳng thức.

Ví dụ:

Nếu 3 > 2, thì

$3^2 > 2^2$

(tức 9 > 4).

4. Ứng dụng của bất đẳng thức

Bất đẳng thức không chỉ tồn tại trong lý thuyết toán học mà còn có nhiều ứng dụng thực tiễn trong đời sống và các lĩnh vực chuyên môn. Dưới đây là một số ứng dụng tiêu biểu:

4.1. Trong toán học

Giải phương trình và bất phương trình. Ví dụ như xác định khoảng nghiệm của bất phương trình

$x^2 – 4x + 3 > 0$

Chứng minh toán học. Ví dụ như chứng minh bất đẳng thức Cauchy-Schwarz hoặc bất đẳng thức tam giác.

4.2. Trong thực tế

• Tối ưu hóa:

Bất đẳng thức giúp giải quyết các bài toán tối ưu hóa nhằm tìm ra phương án tốt nhất với các ràng buộc cụ thể.

• • • Tối ưu chi phí sản xuất với ngân sách có hạn.
    • Xác định khoảng cách ngắn nhất giữa hai địa điểm.
    • Tính toán thời gian nhanh nhất để hoàn thành công việc.

• Đánh giá và phân tích dữ liệu:

Trong các lĩnh vực kỹ thuật, bất đẳng thức hỗ trợ trong việc đặt giới hạn sai số, kiểm tra tính chính xác hoặc an toàn của một hệ thống.

4.3. Trong các lĩnh vực khác

• Khoa học dữ liệu:

Bất đẳng thức được áp dụng trong các thuật toán học máy (machine learning), phân tích dữ liệu và tối ưu hóa mô hình dự đoán.

• Kinh tế học:

Bất đẳng thức được sử dụng để phân tích các giới hạn tài nguyên, tối ưu hóa lợi nhuận hoặc kiểm soát rủi ro trong tài chính.

• Vật lý và kỹ thuật:

Các bất đẳng thức hỗ trợ trong việc thiết lập các giới hạn vật lý, chẳng hạn như công suất tối đa, áp suất hoặc nhiệt độ trong một hệ thống.

5. Bài tập ví dụ về bất đẳng thức

10 Bài tập trắc nghiệm về bất đẳng thức

Bài 1: Cho bất đẳng thức 5x − 3 > 7. Tìm tập nghiệm của x.

A. x > 2

B. x < 2

C. $x>1$

D. x < 1.

Đáp án: A

Bài 2: Số nào sau đây thỏa mãn bất đẳng thức $2x+5\le 9$?
A. $x=2$

B. x = 1

C. $x=3$

D. $x=4.$

Đáp án: B

Bài 3: Cho bất đẳng thức

$x^2 > 9$

. Giá trị nào của $x$ thỏa mãn?

A. $x=2$

B. $x=-4$

C. $x=3$

D. $x=-3$

Đáp án: B

Bài 4: Tập nghiệm của bất đẳng thức $3(x-2)<9$ là:

A. $x>5$

B. x < 5

C. x > 4

D. $x<4$

Đáp án: D

Bài 5: Cho a > b và c < 0. Điều nào sau đây đúng?

A. $ac>bc$

B. $ac<bc$

C. $ac=bc$

D. Không xác định

Đáp án: B

Bài 6: Cho bất đẳng thức ∣x − 3∣ < 2. Tập nghiệm của $x$ là:

A. $1<x<5$

B. $x<1$ hoặc x > 5

C. $x=1$

D. x = 5

Đáp án: A

Bài 7: Chứng minh rằng với mọi $a,b>0$, bất đẳng thức sau luôn đúng:

$\frac{a + b}{2} ≥ \sqrt{ab}$

​. Điều kiện nào xảy ra dấu “=” trong bất đẳng thức này?

A. $a>b$

B. $a=b$

C. $a<b$

D. Không bao giờ xảy ra

Đáp án: B

Bài 8: Cho bất đẳng thức

$x^2 – 6x + 8 ≤ 0$

. Tập nghiệm của bất đẳng thức là:

A. $x<2$ hoặc $x>4$

B. $2\le x\le 4$

C. $x<2$ hoặc x = 4

D. $x>2$ hoặc $x<4$

Đáp án: B

Bài 9: Trong một tam giác, độ dài ba cạnh $a,b,c$ thỏa mãn bất đẳng thức nào sau đây?

A. a + b > c

B. a + b < c

C. $a=b=c$

D. $a+b+c=0$

Đáp án: A

Bài 10: Bất đẳng thức Cauchy-Schwarz áp dụng cho các số dương $a,b,x,y$ là:

$(ax + by)^2 ≤ (a^2 + b^2)(x^2 + y^2)$

. Trường hợp nào bất đẳng thức xảy ra dấu “=”?

A. $a=x$ và $b=y$

B.

$\frac{a}{x} = \frac{b}{y}$

​C. $a+b=x+y$

D. Không xảy ra

Đáp án: B