Tất cả các Công Thức Đạo Hàm đầy đủ nhất [Full]

Tra cứu nhanh các công thức đạo hàm đầy đủ nhất từ cơ bản đến nâng cao. Bảng công thức đạo hàm chi tiết giúp bạn học tập và ứng dụng hiệu quả.

Tìm kiếm: công thức đạo hàm, bảng công thức đạo hàm, đạo hàm cơ bản, đạo hàm nâng cao.

I. Giới thiệu về đạo hàm

Trong toán học, đạo hàm là một trong những khái niệm quan trọng nhất, đóng vai trò nền tảng trong giải tích và có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, kinh tế, kỹ thuật và khoa học dữ liệu. Hiểu và áp dụng thành thạo các công thức đạo hàm không chỉ giúp học sinh, sinh viên giải quyết bài toán nhanh chóng mà còn hỗ trợ trong việc nghiên cứu và phát triển các mô hình tính toán thực tế.

Tuy nhiên, với số lượng lớn công thức đạo hàm từ cơ bản đến nâng cao, việc ghi nhớ và tra cứu đôi khi gây khó khăn cho nhiều người. Chính vì vậy, bài viết này sẽ cung cấp bảng công thức đạo hàm đầy đủ nhất, được hệ thống hóa theo từng nhóm cụ thể. Bạn có thể dễ dàng tham khảo các công thức từ đạo hàm của hàm số cơ bản, hàm số lượng giác, hàm số mũ – logarit, cho đến các quy tắc đạo hàm mở rộng.

II. Định nghĩa và ý nghĩa của đạo hàm

1. Định nghĩa đạo hàm

Trong toán học, đạo hàm là một khái niệm quan trọng trong giải tích, dùng để mô tả tốc độ thay đổi của một hàm số tại một điểm bất kỳ.

Định nghĩa toán học:

Cho hàm số y = f(x), đạo hàm của f(x) tại điểm x₀​ được xác định bằng giới hạn sau:

Trong đó:

• f′(x₀​) là đạo hàm của f(x) tại điểm x₀​.
• Biểu thức trên thể hiện tỉ số giữa sự thay đổi của giá trị hàm số và sự thay đổi rất nhỏ của biến số x.

Nếu giới hạn trên tồn tại, ta nói f(x) có đạo hàm tại x₀​. Khi đó, đạo hàm có thể được coi là hệ số góc của tiếp tuyến tại điểm (x₀​,f(x₀​)) trên đồ thị của hàm số.

2. Ý nghĩa của đạo hàm

a) Ý nghĩa hình học

• Đạo hàm tại một điểm chính là độ dốc của tiếp tuyến với đồ thị của hàm số tại điểm đó.
• Nếu f′(x)>0, đồ thị hàm số đang tăng tại x.
• Nếu f′(x)<0, đồ thị hàm số đang giảm tại x.
• Nếu f′(x)=0, đồ thị có thể đạt cực trị hoặc có điểm uốn.

Ví dụ: Đồ thị của hàm số y=x² có đạo hàm f′(x)=2x. Khi x=0, f′(0)=0, nghĩa là tại điểm này tiếp tuyến song song với trục hoành (cực tiểu).

b) Ý nghĩa vật lý

Trong vật lý, đạo hàm được sử dụng để biểu diễn tốc độ tức thời hoặc sự thay đổi của một đại lượng theo thời gian.

Ví dụ:

• Vận tốc tức thời của một vật đang chuyển động chính là đạo hàm của quãng đường theo thời gian:

v(t)=s′(t)

trong đó s(t)s(t)s(t) là phương trình quãng đường theo thời gian.

• Gia tốc của vật chính là đạo hàm của vận tốc theo thời gian:

a(t)=v′(t)

C) Ứng dụng thực tế của đạo hàm

Ngoài toán học và vật lý, đạo hàm còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác:

• Kinh tế học: Đạo hàm được sử dụng để tính biên lợi nhuận và tối ưu hóa chi phí.
• Kỹ thuật và khoa học máy tính: Đạo hàm giúp tối ưu hóa thuật toán và mạng nơ-ron nhân tạo.
• Sinh học & Y học: Đạo hàm hỗ trợ mô hình hóa sự tăng trưởng của quần thể và phân tích tốc độ lan truyền dịch bệnh.

III. Các công thức đạo hàm cơ bản

Trong toán học, các công thức đạo hàm cơ bản giúp chúng ta tính toán nhanh chóng đạo hàm của những hàm số đơn giản. Đây là nền tảng quan trọng để xây dựng các công thức đạo hàm phức tạp hơn trong giải tích.

1. Đạo hàm của một số hàm cơ bản

Dưới đây là những công thức đạo hàm quan trọng nhất mà bạn cần ghi nhớ:

Bảng công thức đạo hàm cơ bản

Ví dụ:

Đạo hàm của f(x) = x³ là f′(x) = 3x².

Đạo hàm của

$f(x) = \frac{1}{x^5}$

là

$f'(x) = -\frac{5}{x^6}$

2. Đạo hàm của một số hàm căn thức phổ biến

Bảng đạo hàm căn thức bậc 2, bậc n

Ví dụ:

Đạo hàm của

$f(x) = \sqrt[3]{x} = x^{\frac{1}{3}}$

​ là

$f'(x) = \frac{1}{3}x^{-\frac{2}{3}}$

3. Đạo hàm của hàm số mũ và logarit cơ bản

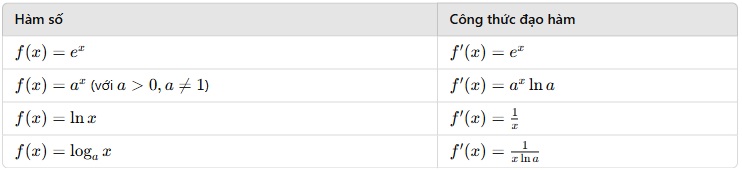
Bảng đạo hàm hàm số mũ và logarit

Ví dụ:

Đạo hàm của f(x) = 2^x là f′(x) = 2^x

Đạo hàm của f(x) = ln⁡(x²) là f′(x) = 2/x​

4. Tóm tắt các công thức đạo hàm cơ bản

Để dễ ghi nhớ, bạn có thể hệ thống hóa các công thức trên thành một nhóm:

• Đạo hàm của hằng số bằng 0.
• Đạo hàm của xⁿ là nxⁿ⁻¹.​
• Đạo hàm của hàm mũ e^x giữ nguyên, còn a^x thì nhân thêm ln a.
• Đạo hàm của logarit tự nhiên là 1/x.

Các công thức này giúp bạn tính nhanh đạo hàm của những hàm đơn giản và là nền tảng để tiếp cận các quy tắc đạo hàm phức tạp hơn trong các phần tiếp theo.

VI. Công thức đạo hàm của các hàm số lượng giác

Hàm số lượng giác xuất hiện phổ biến trong toán học, vật lý, kỹ thuật và nhiều lĩnh vực khác. Việc nắm vững công thức đạo hàm của các hàm số lượng giác giúp bạn giải quyết nhiều bài toán quan trọng.

1. Đạo hàm của các hàm lượng giác cơ bản

Dưới đây là bảng tổng hợp công thức đạo hàm của các hàm lượng giác phổ biến:

Bảng đạo hàm của hàm số lượng giác cơ bản

Ví dụ minh họa: 

Đạo hàm của f(x) = sin2x là f′(x) = 2cos2x (áp dụng quy tắc đạo hàm của hàm hợp)

Đạo hàm của f(x) = tan3x là f′(x) = 3sec²3x

2. Đạo hàm của các hàm lượng giác ngược

Ngoài các hàm lượng giác thông thường, chúng ta còn có các công thức đạo hàm của hàm lượng giác ngược:

Bảng đạo hàm hàm lượng giác ngược

3. Tóm tắt công thức đạo hàm lượng giác

• Đạo hàm của sin là cos, còn của cos là -sin.
• Đạo hàm của tan là sec², còn của cot là -csc².
• Đạo hàm của sec là sec × tan, còn của csc là -csc × cot.
• Đạo hàm của hàm lượng giác ngược chủ yếu có dạng phân số chứa căn hoặc bình phương.

4. Ứng dụng thực tế của đạo hàm lượng giác

• Vật lý: Dùng để tính vận tốc góc và gia tốc góc trong cơ học quay.
• Kỹ thuật: Ứng dụng trong xử lý tín hiệu và dao động điều hòa.
• Toán học: Giải phương trình vi phân, tính giới hạn, và nghiên cứu dao động sóng.

V. Công thức đạo hàm của hàm số mũ và logarit

Hàm số mũ và logarit đóng vai trò quan trọng trong giải tích và ứng dụng trong nhiều lĩnh vực như kinh tế, vật lý, sinh học, và khoa học máy tính. Các công thức đạo hàm của chúng không chỉ dễ ghi nhớ mà còn thường xuyên xuất hiện trong các bài toán thực tế.

1. Đạo hàm của hàm số mũ

Bảng đạo hàm của hàm số mũ

Ví dụ minh họa:

Đạo hàm của f(x)=e^2x là f′(x)=2e^2x

Đạo hàm của $f(x) = 3^{x^2}$

$$f^{\mathrm{\prime }}(x)=3^{x^2}\cdot \ln 3\cdot 2x$$

2. Đạo hàm của hàm số logarit

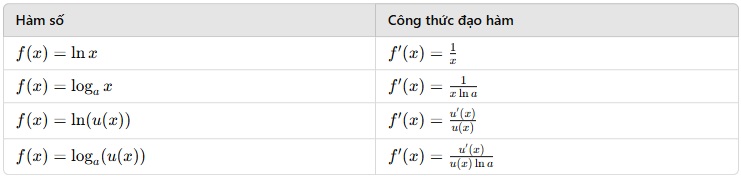
Bảng đạo hàm của hàm số logarit

Ví dụ minh họa:

• Đạo hàm của $f(x)=\ln (2x)\; là$ f′(x) = 2.(1/2x) = 1/x
• Đạo hàm của f(x) = log₂​(x³): f′(x) = 3x² /(x³ln 2) = 3/(xln 2)

​3. Tóm tắt công thức đạo hàm của hàm mũ và logarit

Đạo hàm của hàm mũ:

• Với cơ số tự nhiên e, đạo hàm giữ nguyên: f′(x) = e^x.
• Với cơ số a>0, a≠1, cần nhân thêm lna: f′(x) = a^xlna.

Đạo hàm của hàm logarit:

• Logarit tự nhiên ln x = f′(x) = 1/x.
• Logarit cơ số a: f′(x) = 1/(xln a).

Với hàm hợp, cần áp dụng quy tắc đạo hàm hàm hợp:

• f(x)=e^u(x): f′(x) = e^u(x) .u′(x)
• f(x) = ln(u(x)): f′(x) = u′(x)/u(x)

4. Ứng dụng thực tế của đạo hàm hàm mũ và logarit

Kinh tế học:

• Đạo hàm hàm mũ được dùng để tính lãi kép, tăng trưởng dân số, hoặc phân tích tỷ suất sinh lời.
• Đạo hàm của logarit dùng để đo lường tốc độ thay đổi phần trăm (hàm co giãn).

Khoa học và kỹ thuật:

• Hàm mũ mô tả sự phân rã phóng xạ hoặc sự phát triển của vi khuẩn.
• Hàm logarit được sử dụng trong xử lý tín hiệu, quy mô, và thang đo logarit (ví dụ: decibel).

Khoa học dữ liệu:

• Hàm logarit hỗ trợ tính log-loss trong tối ưu hóa mô hình học máy.
• Hàm mũ giúp xử lý hàm kích hoạt trong mạng nơ-ron nhân tạo.

VI. Công thức đạo hàm của hàm số hyperbolic

Hàm số hyperbolic (hay hàm số siêu việt) là một nhóm các hàm toán học liên quan chặt chẽ đến hàm số lượng giác. Chúng thường được sử dụng trong các lĩnh vực như kỹ thuật, vật lý, và tính toán số học. Việc nắm vững công thức đạo hàm của các hàm hyperbolic giúp bạn xử lý các bài toán phức tạp trong phân tích.

1. Đạo hàm của các hàm hyperbolic cơ bản

Các công thức đạo hàm của hàm số hyperbolic cơ bản bao gồm:

Lưu ý:

Các hàm hyperbolic liên quan mật thiết đến hàm số mũ với công thức:

sinhx=(e^x−e^−x)/2​, coshx=(e^x+e^−x)/2​, tanhx = sinhx/coshx​

Ví dụ minh họa về đạo hàm của hàm hyperbolic cơ bản:

$f(x)=\sinh (2x)$: f′(x)=2cosh(2x)

$f(x)=\text{sech}($x²$)$:f′(x)=−2x⋅sech(x²$$)\cdot \tanh ($$x²$$)$$

2. Đạo hàm của các hàm hyperbolic ngược

Ngoài các hàm cơ bản, đạo hàm của các hàm hyperbolic ngược cũng rất quan trọng:

$\mathrm{arsinh}(x)$: Hàm hyperbolic nghịch đảo của $\sinh (x)$, xác định trên toàn bộ $\mathbb{R}$.

$$f'(x) = \frac{1}{\sqrt{x^2 + 1}}$$

​$\mathrm{arcosh}(x)$: Hàm hyperbolic nghịch đảo của $\cosh (x)$, xác định khi x>1.

$$f'(x) = \frac{1}{\sqrt{x^2 – 1}}$$

​$\mathrm{artanh}(x)$: Hàm hyperbolic nghịch đảo của tanh(x), xác định khi $|x|<1$.

$$f'(x) = \frac{1}{1 – x^2}$$

​arcoth(x): Hàm hyperbolic nghịch đảo của coth(x), xác định khi $|x|>1$.

$$f'(x) = \frac{1}{1 – x^2}$$

​$\mathrm{arsech}(x)$: Hàm hyperbolic nghịch đảo của $\mathrm{sech}(x)$, xác định khi 0<x≤1.

$$f'(x) = -\frac{1}{x \sqrt{1 – x^2}}$$

​$\mathrm{arcsch}(x)$: Hàm hyperbolic nghịch đảo của $\mathrm{csch}(x)$, xác định trên toàn bộ $\mathbb{R}\setminus \{0\}$.

$$f'(x) = -\frac{1}{|x| \sqrt{1 + x^2}}$$

Ví dụ về đạo hàm của hàm hyperbolic ngược:

$f(x)=\text{arsinh}(x^2)$

$$f'(x) = \frac{2x}{\sqrt{x^4 + 1}}$$

​$f(x)=\text{arcosh}(3x)$:

$$f'(x) = \frac{3}{\sqrt{(3x)^2 – 1}}$$

3. Tóm tắt công thức đạo hàm của hàm hyperbolic

• Đạo hàm của $\sinh x$ và $\cosh x$ giống như hoán đổi vai trò, không thay đổi dấu.
• Đạo hàm của $\tanh x$ và $\coth x$ liên quan đến bình phương các hàm số hyperbolic.
• Các công thức đạo hàm của hàm hyperbolic ngược thường có dạng phân số chứa căn hoặc bình phương.

4. Ứng dụng của đạo hàm hàm số hyperbolic

• Kỹ thuật: Hàm hyperbolic được sử dụng để mô tả chuyển động tuyến tính, dao động, hoặc sự phân bố nhiệt trong vật liệu.
• Xử lý ảnh: Được ứng dụng trong tăng cường độ sáng hoặc áp dụng các bộ lọc không gian.
• Khoa học dữ liệu: Các hàm hyperbolic thường được sử dụng làm hàm kích hoạt (activation function) trong mạng nơ-ron nhân tạo, ví dụ như hàm tanhx.

VII. Các quy tắc đạo hàm quan trọng

Trong giải tích, việc tính đạo hàm không chỉ dừng lại ở các công thức cơ bản mà còn đòi hỏi sự kết hợp của nhiều quy tắc tính đạo hàm. Hiểu và vận dụng đúng các quy tắc này sẽ giúp giải quyết được các bài toán phức tạp một cách nhanh chóng và chính xác.

1. Quy tắc đạo hàm của tổng và hiệu

Quy tắc tổng: Đạo hàm của tổng hai hàm số bằng tổng đạo hàm của từng hàm.

$$\left( f(x) + g(x) \right)’ = f'(x) + g'(x)$$

(f(x)+g(x))′=f′(x)+g′(x)

Quy tắc hiệu: Đạo hàm của hiệu hai hàm số bằng hiệu đạo hàm của từng hàm.

$$\left( f(x) – g(x) \right)’ = f'(x) – g'(x)$$

(f(x)−g(x))′=f′(x)−g′(x)

Ví dụ minh họa:

Tính đạo hàm của: f(x)=x³+2x²−5x

=> f′(x)=3x²+4x−5

2. Quy tắc nhân (Product Rule)

Khi cần đạo hàm tích của hai hàm số, áp dụng công thức:

(f(x)⋅g(x))′=f′(x)⋅g(x)+f(x)⋅g′(x)

Ví dụ minh họa:

Tính đạo hàm của f(x)=x²⋅e^x

=> f′(x) = 2x⋅e^x+x²⋅e^x = e^x(2x+x²)

3. Quy tắc thương (Quotient Rule)

Đạo hàm của thương hai hàm số được tính theo công thức:

$$\left( \frac{f(x)}{g(x)} \right)’ = \frac{f'(x) \cdot g(x) – f(x) \cdot g'(x)}{\left( g(x) \right)^2}, \; g(x) \neq 0$$

(f(x)/g(x)​)′= [f′(x)⋅g(x)−f(x)⋅g′(x)]​/(g(x))²$$,g(x)$$≠ $$0$$

Ví dụ minh họa:

• Tính đạo hàm của f(x) = x²/sinx​:

=> f′(x) = (2x⋅sinx−x²⋅cosx)/sin²x

4. Quy tắc hàm hợp (Chain Rule)

Khi một hàm số được viết dưới dạng hợp của hai (hoặc nhiều) hàm số, sử dụng quy tắc hàm hợp:

$$\left( f(g(x)) \right)’ = f'(g(x)) \cdot g'(x)$$

(f(g(x)))′ = f′(g(x))⋅g′(x)

Ví dụ minh họa:

Tính đạo hàm của $f(x)=\ln (3$x²$+1)$:

$$f'(x) = \frac{1}{3x^2 + 1} \cdot 6x = \frac{6x}{3x^2 + 1}$$

​

5. Quy tắc đạo hàm lũy thừa của hàm số

Nếu f(x) =(u(x))ⁿ, thì:

f′(x)=n⋅(u(x))^n-1⋅u′(x)

Ví dụ minh họa:

Tính đạo hàm của f(x)=(x²+3x)⁴

$$f'(x) = 4 \cdot \left( x^2 + 3x \right)^3 \cdot \left( 2x + 3 \right)$$

=> f′(x) = 4⋅(x²+3x)³⋅(2x+3)

6. Tóm tắt các quy tắc đạo hàm quan trọng

• Quy tắc tổng và hiệu: Đơn giản cộng hoặc trừ từng đạo hàm.
• Quy tắc nhân: Tính theo công thức f′(x)⋅g(x) + f(x)⋅g′(x).
• Quy tắc thương: Phải trừ và chia bình phương mẫu.
• Quy tắc hàm hợp: Áp dụng khi hàm có cấu trúc lồng nhau.
• Quy tắc lũy thừa: Áp dụng với hàm dạng (u(x))ⁿ

VIII. Các đạo hàm cao cấp và đạo hàm cấp cao

Khi xét đến các bài toán phức tạp trong giải tích, chúng ta thường cần đến khái niệm đạo hàm cao cấp (hay còn gọi là đạo hàm bậc cao). Đây là quá trình tiếp tục lấy đạo hàm của một hàm đã được đạo hàm trước đó. Việc nắm vững kiến thức về đạo hàm cao cấp giúp giải quyết các bài toán liên quan đến sự thay đổi phức tạp của hàm số.

1. Định nghĩa đạo hàm cao cấp

• Đạo hàm cấp 1 (hay đạo hàm bậc 1): Là đạo hàm thông thường của hàm số $f(x)$.
  Ký hiệu: f′(x).

• Đạo hàm cấp 2: Là đạo hàm của f′(x), ký hiệu là f′′(x) hoặc d²f​/dx²

• Đạo hàm cấp $n$: Là đạo hàm của f⁽ⁿ⁻¹⁾(x), ký hiệu là f⁽ⁿ⁾(x) hoặc dⁿf​/dxⁿ

Công thức tổng quát:

Nếu $f(x)$ khả vi $n$-lần, thì:

$$f^{(n)}(x) = \frac{d^n f(x)}{dx^n}.$$

2. Một số công thức đạo hàm cao cấp thông dụng

Đạo hàm cao cấp của đa thức:

Với hàm số f(x)=axⁿ

$$f^{(k)}(x) = \frac{n!}{(n-k)!} \cdot a \cdot x^{n-k}, \; (k \leq n).$$Nếu $k>n$, thì f^(k)(x)=0

Ví dụ:

Tính đạo hàm cấp 3 của f(x)=2x⁵

$$f”'(x) = \frac{5 \cdot 4 \cdot 3}{1} \cdot 2x^{5-3} = 120x^2.$$Đạo hàm cao cấp của hàm mũ:

Với $f(x)=$e^x: $$f^{(n)}(x) = e^x, \; \forall n.$$

Đạo hàm cao cấp của hàm lượng giác:

• Với $f(x)=\sin x$: $$f^{(n)}(x) = \sin\left(x + \frac{n\pi}{2}\right).$$
  
• Với $f(x)=\cos x$: $$f^{(n)}(x) = \cos\left(x + \frac{n\pi}{2}\right).$$
  

Ví dụ:

Tính đạo hàm cấp 4 của $f(x)=\cos x$: $$f^{(4)}(x) = \cos x.$$

3. Ứng dụng của đạo hàm cao cấp

Tính chất hình học của đồ thị hàm số:

Đạo hàm bậc cao giúp phân tích độ cong của đồ thị (hình dạng uốn lượn), đặc biệt trong khảo sát sự biến thiên của hàm số.

Chuỗi Taylor và chuỗi Maclaurin:

Đạo hàm bậc cao được sử dụng để xây dựng các chuỗi số giúp xấp xỉ giá trị hàm số tại một điểm.

Ví dụ: $$f(x) \approx f(a) + f'(a)(x-a) + \frac{f”(a)}{2!}(x-a)^2 + \dots$$

Cơ học và vật lý:

Đạo hàm cấp 2 biểu diễn gia tốc trong chuyển động, đạo hàm cấp 3 biểu diễn sự thay đổi gia tốc (giật).

Lập trình mô phỏng:

Các thuật toán xử lý hình ảnh hoặc mô phỏng trong game thường sử dụng đạo hàm bậc cao để điều chỉnh các yếu tố phức tạp.

4. Một số bài tập thực hành

• Tính đạo hàm cấp 3 của f(x) = 4x⁴−2x²+1
• Chứng minh rằng đạo hàm cấp $n$ của f(x) = e^2x là f⁽ⁿ⁾(x) = 2ⁿe^2x.
• Tìm đạo hàm cấp 4 của $f(x)=\sin (3x)$.

5. Tóm tắt các điểm chính về đạo hàm cao cấp

• Đạo hàm cấp $n$ là quá trình lấy đạo hàm liên tiếp $n$-lần.
• Đạo hàm cao cấp có ứng dụng rộng rãi trong toán học, vật lý, kỹ thuật và lập trình.
• Hiểu rõ các công thức và tính chất của đạo hàm cao cấp giúp giải quyết các bài toán phức tạp hiệu quả hơn.

IX. Lời kết

Trong bài viết này, chúng ta đã cùng tìm hiểu toàn bộ các công thức đạo hàm từ cơ bản đến nâng cao, bao gồm cả các hàm số lượng giác, hàm số mũ, logarit, và hyperbolic. Đồng thời, các quy tắc đạo hàm quan trọng như quy tắc tổng, hiệu, nhân, thương và hàm hợp cũng được giải thích chi tiết kèm theo ví dụ minh họa thực tế. Cuối cùng, chúng ta đã khám phá khái niệm và ứng dụng của đạo hàm cao cấp trong toán học cũng như các lĩnh vực khoa học, kỹ thuật.

Việc nắm vững hệ thống các công thức đạo hàm không chỉ giúp bạn giải quyết các bài toán giải tích một cách hiệu quả mà còn là công cụ mạnh mẽ để nghiên cứu và ứng dụng trong nhiều lĩnh vực thực tiễn như vật lý, kinh tế, và lập trình.

Nếu bạn cảm thấy bài viết này hữu ích, hãy chia sẻ để nhiều người hơn có thể tiếp cận bài viết này. Đừng quên khám phá thêm các bài viết liên quan trên website của chúng tôi để trau dồi thêm kiến thức và kỹ năng về toán học.