Diện tích tam giác đều – Công thức, cách tính và bài tập

Diện tích tam giác đều là gì? Công thức tính diện tích tam giác đều, cách tính chi tiết, ví dụ minh họa và bài tập trắc nghiệm có đáp án.

1. Tam giác đều là gì?

1.1. Khái niệm tam giác đều?

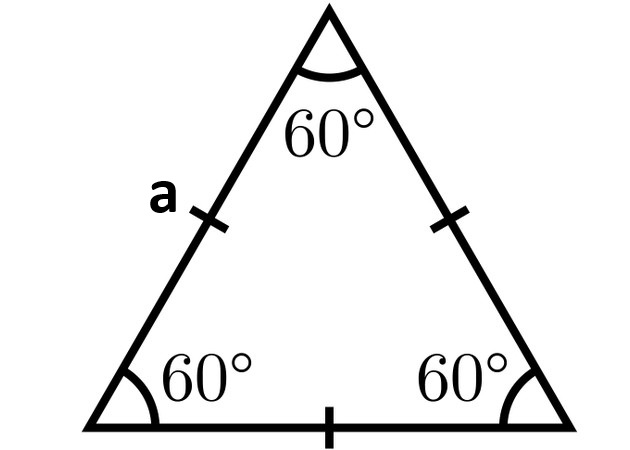
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau. Đây là một dạng đặc biệt của tam giác, có nhiều tính chất đối xứng và được sử dụng rất nhiều trong các bài toán liên quan đến chu vi và diện tích, đặc biệt là bài toán diện tích tam giác đều.

Hình ảnh tam giác đều có độ dài cạnh là a

1.2. Đặc điểm của tam giác đều

Tam giác đều có những đặc điểm quan trọng sau:

• Ba cạnh bằng nhau

• Ba góc bằng nhau, mỗi góc có số đo là 60°

• Đường cao, trung tuyến, đường phân giác và đường trung trực trùng nhau

Nhờ những đặc điểm này, việc tính toán trong tam giác đều trở nên đơn giản và chính xác hơn so với các loại tam giác khác.

1.3. Ý nghĩa của tam giác đều trong bài toán diện tích

Việc xác định đúng tam giác đều có ý nghĩa rất quan trọng, bởi:

• Tam giác đều có công thức tính diện tích riêng

• Có thể tính diện tích chỉ cần biết độ dài một cạnh

• Giúp học sinh tránh nhầm lẫn với tam giác cân hoặc tam giác thường

Chính vì vậy, trước khi học cách tính diện tích tam giác đều, các bạn cần nắm vững khái niệm và đặc điểm của tam giác đều để áp dụng công thức đúng và hiệu quả.

2. Diện tích tam giác đều là gì?

2.1. Định nghĩa diện tích tam giác đều

Diện tích tam giác đều là độ lớn của phần mặt phẳng được giới hạn bởi ba cạnh của tam giác đều. Nói cách khác, diện tích cho biết tam giác đều chiếm bao nhiêu đơn vị diện tích trên mặt phẳng.

Công thức diện tích tam giác đều S, có độ dài cạnh là a

Trong toán học, diện tích tam giác đều thường được ký hiệu là S và được tính bằng đơn vị diện tích như:

• xentimét vuông (cm²),

• mét vuông (m²),

• hoặc các đơn vị diện tích khác phù hợp với bài toán.

2.2. Ý nghĩa của diện tích tam giác đều

Việc học và hiểu diện tích tam giác đều có ý nghĩa quan trọng trong cả hình học lẫn đời sống thực tế.

Trong học tập:

• Là kiến thức trọng tâm trong chương trình Toán tiểu học và trung học cơ sở

• Giúp học sinh rèn luyện kỹ năng vận dụng công thức hình học

• Là nền tảng để học các bài toán liên quan đến tam giác, đa giác và hình phẳng

Trong thực tế:

• Dùng để tính diện tích các vật, mặt phẳng có dạng tam giác đều

• Ứng dụng trong thiết kế, xây dựng, kiến trúc và mỹ thuật

• Giúp giải quyết các bài toán đo đạc, ước lượng diện tích

Như vậy, nắm vững khái niệm và ý nghĩa của diện tích tam giác đều sẽ giúp học sinh hiểu đúng bản chất, từ đó dễ dàng tiếp cận công thức tính diện tích tam giác đều và các dạng bài tập vận dụng ở những phần tiếp theo.

3. Công thức tính diện tích tam giác đều

3.1. Công thức chuẩn SGK

Giả sử tam giác đều có độ dài mỗi cạnh là a (đơn vị đo độ dài tùy theo đề bài), thì diện tích tam giác đều được tính theo công thức:

$$S = \frac{a^2\sqrt{3}}{4}$$

Trong đó:

• S là diện tích tam giác đều

• a là độ dài cạnh tam giác đều

• √3 là căn bậc hai của 3

3.2. Giải thích nguồn gốc công thức

Công thức diện tích tam giác đều được suy ra từ công thức diện tích tam giác nói chung:

$$S = \frac{1}{2} \times \text{đáy} \times \text{chiều cao}$$

Với tam giác đều:

• Mỗi cạnh đều có thể chọn làm đáy

• Chiều cao hạ từ một đỉnh sẽ chia tam giác đều thành hai tam giác vuông bằng nhau

Chiều cao của tam giác đều cạnh a được xác định theo định lý Pythagore:

$$h = \frac{a\sqrt{3}}{2}$$

​​

Thay vào công thức diện tích:

$$S = \frac{1}{2} \times a \times \frac{a\sqrt{3}}{2} = \frac{a^2\sqrt{3}}{4}$$

​

3.3. Đơn vị diện tích khi tính diện tích tam giác đều

Khi áp dụng công thức tính diện tích tam giác đều, cần lưu ý:

• Nếu cạnh a đo bằng cm → diện tích tính bằng cm²

• Nếu cạnh a đo bằng m → diện tích tính bằng m²

Việc đổi đơn vị độ dài phải thực hiện trước khi tính diện tích để tránh sai sót – đây là lỗi học sinh thường gặp trong các bài tập trắc nghiệm.

B.

$S={\displaystyle \frac{a^2\sqrt{3}}{4}}$

C.

$S = \dfrac{a\sqrt{3}}{2}$

D.

$S = \dfrac{a^2}{2}$